반응형
- 2진 탐색 알고리즘 (Binary Search Algorithm)
2진 트리 알고리즘은 값이 정렬되어 있을 때 사용 가능한 검색 알고리즘 입니다.
순차(선형) 검색 알고리즘과 달리 리스트 앞부터 순차적으로 값을 찾는 방법이 아니무로 리스트가 길이가 길수록 순차 검색 알고리즘보다 빨리 검색 할 수 있습니다.
<검색 알고리즘>
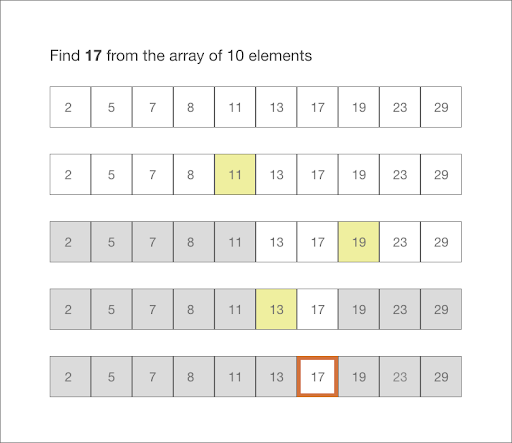
위 그림을 보면서 설명 하도록 하겠습니다. 리스트 길이는 10이고 그 중 정수 17을 찾는 방법입니다.
1. 찾고자 하는 범위에 중간의 Index 값(11)을 확인 합니다. -----> 2번째 List 그림
2. 1번에서 찾은 값(11)이 찾고자하는 값(17)이 아닐경우 1번에서 찾은 값(11)과 찾고자하는 값이(17) 비교하여 찾는 값이 크면 왼쪽의 범위를 배제하고, 작을 경우 오른쪽 범위를 배제합니다 -----> 3번째 List 그림
3. 그리고 다시 남은 범위의 중간을 구하고 그 값이 찾고자하는 값이 아니면 2 번 방법으로 다시 범위를 좁힙니다.
<2진 탐색 알고리즘 Code>
public class BinarySearch {
private static int count = 1;
public static void main(String[] args) {
int[] dataArray = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
System.out.print("검색할 데이터를 입력하세요 : ");
Scanner scan = new Scanner(System.in);
int search = Integer.parseInt(scan.next());
scan.close();
int result = binarySearch(dataArray, search);
if (result == -1) {
System.out.println("데이터를 찾지 못하였습니다");
} else {
System.out.println("데이터의 index는 " + result + " 입니다.");
}
System.out.println("갬색 횟 수 : " + count);
}
public static int binarySearch(int[] arr, int search) {
int low = 0;
int mid = 0;
int high = arr.length;
while (low <= high) {
mid = (low + high) / 2;
if (arr[mid] < search) {
low = mid + 1;
} else if (arr[mid] > search) {
high = mid - 1;
} else {
return mid;
}
++count;
}
return -1;
}
}
반응형
'Tech > 알고리즘' 카테고리의 다른 글
| 삽입 정렬(Insertion Sort) (0) | 2020.06.01 |
|---|---|
| 선택정렬(SelectionSort) (0) | 2020.06.01 |
| 버블정렬 (BubbleSort) (0) | 2020.06.01 |
| 2진 탐색 트리 알고리즘 (Binary Search Tree) (0) | 2020.05.26 |
| 순차 검색 알고리즘 (Sequential Search) (0) | 2020.05.26 |




댓글