
- 실수를 표현 하는 방법
<부동 소수>
-
소수점이 이동 가능하다고 해서 붙여진 이름이다.
-
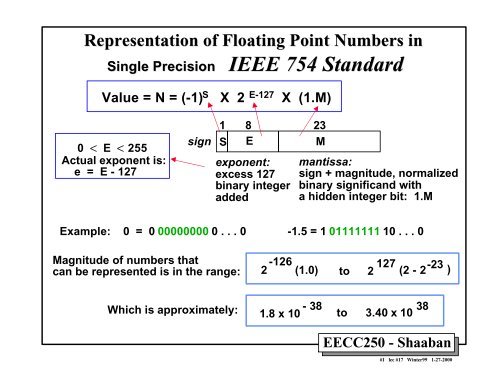
32비트로 되어있으며 부호부에 1비트, 지수부에 8비트, 가수부에 23비트를 할당하는 표현 방식을 말한다.
- 부동 소수를 사용해도 실수를 정확하게 표현 할 수 없다. 그 이유는 2진수로 소수를 정확하게 표현할 수 없기 때문이다.
<부동 소수 2진수 표현 방밥>
float 값인 6.25f를 2진수를 표현하는방법은 지수부(정수)6, 과 가수부(실수)0.25를 나누어서 표현한다. 지수부는 2진수로 변환하면 된다 그럼 110 (6) -> 1* (2^2) + 1 * (2^1) + 0 * (2^0) 가 되고, 가수 부분은 가수 를 2를곱하고 -1을 했을때 0이 될때까지 계속 2를 곱해여 정수 부분 수를 나열하는 방법이다.
ex)0.3 을 2진수로 변경하면 0.3 * 2 = 0.6 (0) => 0.6 * 2 (1) => 0.2 * 2 (0) => 0.4 * 2 (0) => 0.8 * 2 (1) => 0.6 * 2 (1) => 0.2 * 2 (0) => 0.4 * 2 (0) 0.8 * 2 (1) ........ 0100110011
예제를 보면 알듯이 값이 무한적으로 반복하는 것을 볼 수 있다. 이렇게 때문에 실수를 2진수로 정확하게 표현 할 수 없는 것이다.
public class FloatingPoint {
public static float a = 6.52f;
public static void main(String[] args) {
int b = (int) Math.floor(a); // 지수
float c = a - b; // 가수
System.out.println("지수 : " + b);
System.out.println("가수 : " + c);
// 지수 부분
StringBuilder sb = new StringBuilder();
while(b != 0) {
int d = b%2;
b = b/2;
sb.append(d);
}
int count = 0;
StringBuilder sb2 = new StringBuilder();
while(c != 0.0) {
float e = c *2;
if ((e - 1) == 0.0) {
break;
} else {
sb2.append((int)Math.floor(e));
c = Float.parseFloat(String.format("%.2f", (e >= 1) ? (e-1) : e));
}
count++;
if (count == 23) break; // 지정하지 안으면 무한 루프로 돌 수 있다.
}
System.out.println("지수 : " + sb.reverse().toString());
System.out.println("가수 : " + sb2.reverse().toString());
}
}위에 코드는 실수를 2진수 표현으로 반환하는 코드이다.
public class FloatingPoint {
public static void main(String[] args) {
// Double
Double sum_1 = 0.0;
for (int i=0 ; i<100; i++) {
sum_1 += 0.2;
}
System.out.println("Dobule 0.1 100번 더함, 0.1*100 : "+sum_1 + " , "+ (0.1f*100));
// Float
Float sum_2 = 0.0f;
for (int i=0 ; i<100; i++) {
sum_2 += 0.2f;
}
System.out.println("Float 0.1f 100번 더함, 0.1*100 : "+sum_2 + " , "+ (0.1*100));
Double sum_3 = 0.0;
for(int b=0; b<100; b++) {
BigDecimal value1 = new BigDecimal(sum_3.toString());
sum_3 = value1.add(new BigDecimal("0.1")).doubleValue();
}
System.out.println("BigDecimal '0.1' 100더함 , 0.1*100 : "+sum_3 + " , "+ (0.1*100));
}
}실행결과
Dobule 0.1 100번 더함, 0.1*100 : 19.99999999999996 , 10.0
Float 0.1f 100번 더함, 0.1*100 : 20.000004 , 10.0
BigDecimal '0.1' 100더함 , 0.1*100 : 10.0 , 10.0자료형의 가수 부분이 커지면 실수를 표현하는 정확도는 올라가지만 그래도 정확하게 값을 표현 할 수 는 없다.
위와같은 문제 때문에 정밀한 숫자계산을 필요한 영역에서는 BigDecimal을 사용한다.
'Tech > Java' 카테고리의 다른 글
| Java 자료구조 - Queue (0) | 2020.05.25 |
|---|---|
| Java 자료구조 - Stack (0) | 2020.05.25 |
| Java 참조 자료형(클래스, 인터페이스, 배역, 열겨 타입) (0) | 2020.05.23 |
| Java 기본 자료형 (0) | 2020.05.23 |
| JVM 더 깊이 있게 알아보자 (0) | 2020.05.22 |




댓글